이제 회로를 분석하기에 몇가지 분류를 하고 진행하자.
[회로 특성 고려]
1) 회로의 loss를 전부 고려할 것이에요. (general loss = lossy)
2) 회로의 loss를 전혀 고려하지 않을 것이에요. (lossless , ideal)
3) 약간의 loss가 있다고 생각할 것이에요. (low loss)
[Load Impedance 고려]
1) Impedance가 short
2) Impedance가 open
3) Impedance가 matching
[TL 길이 고려]
1) $\Delta z$ = $\frac{4}{\lambda}$
2) $\Delta z$ = $\frac{2}{\lambda}$
0. 가장 일반적인 lossy 전송선로를 분석해보자. 즉, 회로의 loss를 전부 고려하겠다.
1.
Transmission Line (1)의 [그림 3]을 가져와서 KVL, KCL을 해석해보자. 다시 한 번 말하지만 $\Delta z$가 작을 때만 이 해석이 가능하다.
- Equation 1. KVL 적용

양 변을 $\Delta z$로 나눠주자.

$\Delta z$가 0에 가까워질수록 KVL, KCL을 이용한 분석이 정확해진다. 이를 이용해 극한값을 취한다.

도함수의 정의에 따라 좌변은 z의 변화에 대한 v(z)의 변화로 나타낼 수 있겠다.

- Equation 2. KCL 적용





2.
KVL, KCL에 의해 정리된 식은 아래와 같다.


z에 관한 편미분 식과 t에 관한 편미분 식이 공존한다. 이를 간소화하기 위해 푸리에 변환을 이용해서 t에 관한 편미분 방정식을 복소수 jω텀으로 변환할 수 있다.


위의 두 식을 각각 [Eq3], [Eq4]로 설정하겠다. 이제 이 미분 방정식을 V와 I에 대해서 풀기만 하면 된다.
3.
[Eq3]을 z에 대해 한 번 더 미분한다.

이 식에 [Eq4]를 대입한다.

우변을 모두 좌변으로 넘기면 일반적인 homogeneous Equation이 완성된다.

이런 형태의 미분방정식을 푸는 방법은

으로 설정해주고 각각 $Ae^{-kz} + Be^{kz}$임을 이용하자.

4.
전압에 관한 편미분 방정식을 풀었으니 이번에는 전류에 관한 편미분 방정식을 풀어보자. 먼저 [Eq3]에서 시작하자.

이 식을 I(z)에 대해서 정리하면

3.에서 구한 V(z)를 대입하자.

우리가 $\gamma$로 정의한 값은 아래와 같으므로 이를 약분하면
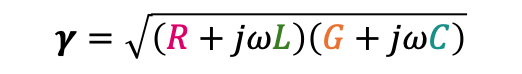

이때 $Z_0$를 다음과 같이 정의하면
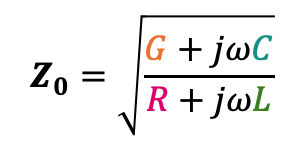
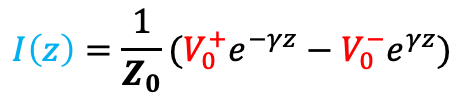
5.
결과만 정리하자면, 전압과 전류에 관한 방정식과 두 가지 상수 propagation constant와 Characteristic Impedance는 다음과 같다.

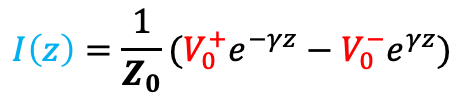
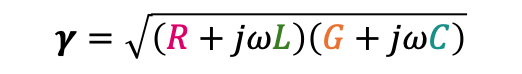
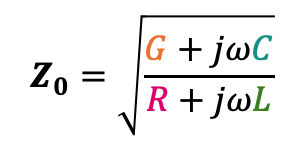
'마이크로파공학' 카테고리의 다른 글
| Transmission Line (5) (0) | 2025.04.02 |
|---|---|
| Transmission Line (4) (0) | 2025.04.02 |
| Transmission Line (3) (0) | 2025.04.01 |
| Transmission Line (1) (0) | 2025.03.29 |
| Introduction of Microwave (0) | 2025.03.29 |




